Semi-Classical Dispersive Estimates for the Wave and Schr¨odinger Equations with a Potential in Dimensions 𓃠≥ 4
-
F. Cardoso
 fernando@dmat.ufpe.br
fernando@dmat.ufpe.br
-
G. Vodev
 georgi.vodev@math.univ-nantes.fr
georgi.vodev@math.univ-nantes.fr
Downloads
Abstract
We expand the operators 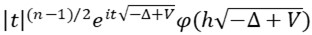 and
and 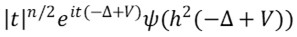 , 0 < h ≪ 1, modulo operators whose L1 → L∞ norm is ON(hN), ∀ N ≥ 1, where ðœ‘, 𜓠∈
, 0 < h ≪ 1, modulo operators whose L1 → L∞ norm is ON(hN), ∀ N ≥ 1, where ðœ‘, 𜓠∈ 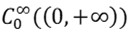 and V ∈ L∞(ð“¡ð“ƒ), 𓃠≥ 4, is a real-valued potential satisfying V(x) = O (〈x〉-ð›¿), 𛿠> (𓃠+ 1)/2 in the case of the wave equation and 𛿠> (𓃠+ 2)/2 in the case of the Schr¨odinger equation. As a consequence, we give sufficent conditions in order that the wave and the Schr¨odinger groups satisfy dispersive estimates with a loss of ν derivatives, 0 ≤ ν ≤ (𓃠− 3)/2. Roughly speaking, we reduce this problem to estimating the L1 → L∞ norms of a finite number of operators with almost explicit kernels. These kernels are completely explicit when 4 ≤ 𓃠≤ 7 in the case of the wave group, and when 𓃠= 4, 5 in the case of the Schr¨odinger group.
and V ∈ L∞(ð“¡ð“ƒ), 𓃠≥ 4, is a real-valued potential satisfying V(x) = O (〈x〉-ð›¿), 𛿠> (𓃠+ 1)/2 in the case of the wave equation and 𛿠> (𓃠+ 2)/2 in the case of the Schr¨odinger equation. As a consequence, we give sufficent conditions in order that the wave and the Schr¨odinger groups satisfy dispersive estimates with a loss of ν derivatives, 0 ≤ ν ≤ (𓃠− 3)/2. Roughly speaking, we reduce this problem to estimating the L1 → L∞ norms of a finite number of operators with almost explicit kernels. These kernels are completely explicit when 4 ≤ 𓃠≤ 7 in the case of the wave group, and when 𓃠= 4, 5 in the case of the Schr¨odinger group.
Keywords
Similar Articles
- Elena Cordero, Davide Zucco, Strichartz estimates for the Schrödinger equation , CUBO, A Mathematical Journal: Vol. 12 No. 3 (2010): CUBO, A Mathematical Journal
- Fernando Cardoso, Claudio Cuevas, Georgi Vodev, Dispersive Estimates for the Schrödinger Equation with Potentials of Critical Regularity , CUBO, A Mathematical Journal: Vol. 11 No. 5 (2009): CUBO, A Mathematical Journal
- S. H. Mousavizadegan, Matiur Rahman, Nonlinear Instability of Dispersive Waves , CUBO, A Mathematical Journal: Vol. 7 No. 1 (2005): CUBO, A Mathematical Journal
- Cong He, Jingchun Chen, Vlasov-Poisson equation in weighted Sobolev space \(W^{m, p}(w)\) , CUBO, A Mathematical Journal: Vol. 24 No. 2 (2022)
- Mahdi Zreik, On the approximation of the δ-shell interaction for the 3-D Dirac operator , CUBO, A Mathematical Journal: Vol. 26 No. 3 (2024)
- William Greenberg, Michael Williams, Global Solutions of the Enskog Lattice Equation with Square Well Potential , CUBO, A Mathematical Journal: Vol. 9 No. 1 (2007): CUBO, A Mathematical Journal
- Aparajita Dasgupta, M.W. Wong, The semigroup and the inverse of the Laplacian on the Heisenberg group , CUBO, A Mathematical Journal: Vol. 12 No. 3 (2010): CUBO, A Mathematical Journal
- B. C. Das, Soumen De, B. N. Mandal, Wave propagation through a gap in a thin vertical wall in deep water , CUBO, A Mathematical Journal: Vol. 21 No. 3 (2019)
- Peter D. Hislop, Fundamentals of scattering theory and resonances in quantum mechanics , CUBO, A Mathematical Journal: Vol. 14 No. 3 (2012): CUBO, A Mathematical Journal
- Abderemane Morame, Françoise Truc, Accuracy on eigenvalues for a Schrödinger operator with a degenerate potential in the semi-classical limit , CUBO, A Mathematical Journal: Vol. 9 No. 2 (2007): CUBO, A Mathematical Journal
You may also start an advanced similarity search for this article.














