Concentration of solutions of non-linear elliptic equations involving critical Sobolev exponent
-
Man Chun Leung
matlmc@math.nus.edu.sg
Downloads
Abstract
In IRn (n ≥ 3), an interesting property of the semi-linear equation
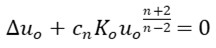
Is that, when K0 is a positive constant, solutions can concentrate at any point. When K0 is not a constant, we show that concentration of solutions requires strong conditions on K0. Through the stereographic projection, the discussion can be extended to Sn, and is related to bubbling, or the blow-up phenomenon.
Keywords
Similar Articles
- Vediyappan Govindan, Choonkil Park, Sandra Pinelas, Themistocles M. Rassias, Hyers-Ulam stability of an additive-quadratic functional equation , CUBO, A Mathematical Journal: Vol. 22 No. 2 (2020)
- George Venkov, Small Data Global Existence and Scattering for the Mass-Critical Nonlinear Schrödinger Equation with Power Convolution in ℳ , CUBO, A Mathematical Journal: Vol. 11 No. 4 (2009): CUBO, A Mathematical Journal
- Gastón E. Hernández, Behavior of multiple solutions for systems of semilinear elliptic equations , CUBO, A Mathematical Journal: No. 11 (1995): CUBO, Revista de Matemática
- Carlos Cesar Aranda, Spacetime singularity, singular bounds and compactness for solutions of the Poisson‘s equation , CUBO, A Mathematical Journal: Vol. 17 No. 2 (2015): CUBO, A Mathematical Journal
- Hatem Mejjaoli, Firdous A. Shah, Nadia Sraieb, Generalized translation and convolution operators in the realm of linear canonical deformed Hankel transform with applications , CUBO, A Mathematical Journal: Vol. 28 No. 1 (2026)
- Elena Cordero, Davide Zucco, Strichartz estimates for the Schrödinger equation , CUBO, A Mathematical Journal: Vol. 12 No. 3 (2010): CUBO, A Mathematical Journal
- Cheok Choi, Gen Nakamura, Kenji Shirota, Variational approach for identifying a coefficient of the wave equation , CUBO, A Mathematical Journal: Vol. 9 No. 2 (2007): CUBO, A Mathematical Journal
- Rafael Galeano, Pedro Ortega, John Cantillo, Stationary Boltzmann equation and the nonlinear alternative of Leray-Schauder type , CUBO, A Mathematical Journal: Vol. 16 No. 1 (2014): CUBO, A Mathematical Journal
- Mihai Prunescu, Concrete algebraic cohomology for the group (â„, +) or how to solve the functional equation ð‘“(ð‘¥+ð‘¦) - ð‘“(ð‘¥) - ð‘“(ð‘¦) = ð‘”(ð‘¥, ð‘¦) , CUBO, A Mathematical Journal: Vol. 9 No. 3 (2007): CUBO, A Mathematical Journal
- Khalil Ezzinbi, Valerie Nelson, Gaston N‘Gu´er´ekata, ð¶â½â¿â¾-Almost Automorphic Solutions of Some Nonautonomous Differential Equations , CUBO, A Mathematical Journal: Vol. 10 No. 2 (2008): CUBO, A Mathematical Journal
<< < 1 2 3 4 5 6 7 8 9 10 11 12 > >>
You may also start an advanced similarity search for this article.
Downloads
Download data is not yet available.
Published
2005-04-01
How to Cite
[1]
M. Chun Leung, “Concentration of solutions of non-linear elliptic equations involving critical Sobolev exponent”, CUBO, vol. 7, no. 1, pp. 1–21, Apr. 2005.
Issue
Section
Articles
