Algorithmic complexity and statistical mechanics
-
Vladimir V'yugin
 vyugin@iitp.ru
vyugin@iitp.ru
-
Victor Maslov
 v.p.maslov@mail.ru
v.p.maslov@mail.ru
Downloads
Abstract
We apply the algorithmic complexity theory to statistical mechanics; in particular, we consider the maximum entropy principle and the entropy concentration theorem for non-ordered data in a non-probabilistic setting. The main goal of this paper is to deduce asymptotic relations for the frequencies of energy levels in a non-ordered collection ωN = [ω1, ..., ωN] from the assumption of maximality of the Kolmogorov complexity K(ωN) given a constraint 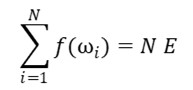 , where E is a number and f is a numerical function; f(ωi) is an energy level. We also consider a combinatorial model of the securities market and give some applications of the entropy concentration theorem to finance.
, where E is a number and f is a numerical function; f(ωi) is an energy level. We also consider a combinatorial model of the securities market and give some applications of the entropy concentration theorem to finance.
Keywords
Similar Articles
- Dmitri V. Alekseevsky, Masoud Ganji, Gerd Schmalz, Andrea Spiro, The Levi-Civita connections of Lorentzian manifolds with prescribed optical geometries , CUBO, A Mathematical Journal: Vol. 26 No. 2 (2024)
- R. Nithya Raj, R. Sundara Rajan, İsmail Naci Cangül, The metric dimension of cyclic hexagonal chain honeycomb triangular mesh and pencil graphs , CUBO, A Mathematical Journal: Vol. 26 No. 3 (2024)
- Chandresh Prasad, P. K. Parida, Steffensen-like method in Riemannian manifolds , CUBO, A Mathematical Journal: Vol. 26 No. 3 (2024)
- Nemri Akram, Retraction Note: Heisenberg-type uncertainty principle for the second \(q\)-Bargmann transform on the unit disk , CUBO, A Mathematical Journal: Vol. 27 No. 1 (2025)
- Jhoan Báez, Luiz A. B. San Martin, Infinitesimally tight Lagrangian submanifolds in adjoint orbits: A classification of real forms , CUBO, A Mathematical Journal: In Press
You may also start an advanced similarity search for this article.














