Regular quaternionic functions and conformal mappings
-
Alessandro Perotti
 perotti@science.unitn.it
perotti@science.unitn.it
Downloads
Abstract
In this paper we study the action of conformal mappings of the quaternionic space on a class of regular functions of one quaternionic variable. We consider functions in the kernel of the Cauchy-Riemann operator
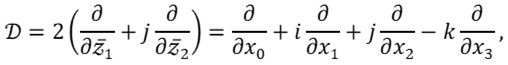
a variant of the Cauchy–Fueter operator. This choice is motivated by the strict relation existing between this type of regularity and holomorphicity w.r.t. the whole class of complex structures on â„. For every imaginary unit p ∈ ð•Š2, let Jp be the corresponding complex structure on â„. Let Holp (ð›º, â„) be the space of holomorphic maps from (ð›º, Jp) to (â„, Lp), where Lp is defined by left multiplication by p. Every element of Holp(ð›º, â„) is regular, but there exist regular functions that are not holomorphic for any p. These properties can be recognized by computing the energy quadric of a function. We show that the energy quadric is invariant w.r.t. three–dimensional rotations of â„. As an application, we obtain that every rotation of the space â„ can be generated by biregular rotations, invertible regular functions with regular inverse. Moreover, we prove that the energy quadric of a regular function can always be diagonalized by means of a three–dimensional rotation.
Keywords
Similar Articles
- N. Seshagiri Rao, K. Kalyani, Fixed point results of \((\phi,\psi)\)-weak contractions in ordered \(b\)-metric spaces , CUBO, A Mathematical Journal: Vol. 24 No. 2 (2022)
- Filippo Cammaroto, Infinitely many solutions for a nonlinear Navier problem involving the \(p\)-biharmonic operator , CUBO, A Mathematical Journal: Vol. 24 No. 3 (2022)
- Mudasir Younis, Nikola Mirkov, Ana Savić, Mirjana Pantović, Stojan Radenović, Some critical remarks on recent results concerning \(\digamma-\)contractions in \(b-\)metric spaces , CUBO, A Mathematical Journal: Vol. 25 No. 1 (2023)
- Ajay Kumar, Ekta Tamrakar, Inertial algorithm for solving split inclusion problem in Banach spaces , CUBO, A Mathematical Journal: Vol. 25 No. 1 (2023)
- Vandana, Rajeev Budhiraja, Aliya Naaz Siddiqui Diop, Curvature properties of \(\alpha\)-cosymplectic manifolds with \(\ast\)-\(\eta\)-Ricci-Yamabe solitons , CUBO, A Mathematical Journal: Vol. 26 No. 1 (2024)
- Seyed Mostafa Sajjadi, Ghasem Alizadeh Afrouzi, On a class of fractional \(p(x,y)-\)Kirchhoff type problems with indefinite weight , CUBO, A Mathematical Journal: Vol. 26 No. 1 (2024)
- Sapan Kumar Nayak, P. K. Parida, Global convergence analysis of Caputo fractional Whittaker method with real world applications , CUBO, A Mathematical Journal: Vol. 26 No. 1 (2024)
- Sirkka-Liisa Eriksson, Heikki Orelma, A simple construction of a fundamental solution for the extended Weinstein equation , CUBO, A Mathematical Journal: Vol. 26 No. 2 (2024)
- Abdoul Aziz Kalifa Dianda, Khalil Ezzinbi, Almost automorphic solutions for some nonautonomous evolution equations under the light of integrable dichotomy , CUBO, A Mathematical Journal: Vol. 27 No. 1 (2025)
- Rubén A. Hidalgo, Una observación sencilla sobre vectores de constantes de Riemann y divisores no-especiales de curvas generalizadas de Fermat , CUBO, A Mathematical Journal: Vol. 27 No. 2 (2025): Spanish Edition (40th Anniversary)
<< < 11 12 13 14 15 16 17 18 > >>
You may also start an advanced similarity search for this article.














