Regular quaternionic functions and conformal mappings
-
Alessandro Perotti
 perotti@science.unitn.it
perotti@science.unitn.it
Downloads
Abstract
In this paper we study the action of conformal mappings of the quaternionic space on a class of regular functions of one quaternionic variable. We consider functions in the kernel of the Cauchy-Riemann operator
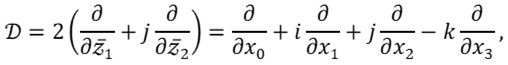
a variant of the Cauchy–Fueter operator. This choice is motivated by the strict relation existing between this type of regularity and holomorphicity w.r.t. the whole class of complex structures on â„. For every imaginary unit p ∈ ð•Š2, let Jp be the corresponding complex structure on â„. Let Holp (ð›º, â„) be the space of holomorphic maps from (ð›º, Jp) to (â„, Lp), where Lp is defined by left multiplication by p. Every element of Holp(ð›º, â„) is regular, but there exist regular functions that are not holomorphic for any p. These properties can be recognized by computing the energy quadric of a function. We show that the energy quadric is invariant w.r.t. three–dimensional rotations of â„. As an application, we obtain that every rotation of the space â„ can be generated by biregular rotations, invertible regular functions with regular inverse. Moreover, we prove that the energy quadric of a regular function can always be diagonalized by means of a three–dimensional rotation.
Keywords
Similar Articles
- B. C. Das, Soumen De, B. N. Mandal, Wave propagation through a gap in a thin vertical wall in deep water , CUBO, A Mathematical Journal: Vol. 21 No. 3 (2019)
- Silvestru Sever Dragomir, Bounds for the generalized \( (\Phi;f) \)-mean difference , CUBO, A Mathematical Journal: Vol. 22 No. 1 (2020)
- T.M.M. Sow, A new iterative method based on the modified proximal-point algorithm for finding a common null point of an infinite family of accretive operators in Banach spaces , CUBO, A Mathematical Journal: Vol. 22 No. 2 (2020)
- Abdi Oli, Kelelaw Tilahun, G. V. Reddy, The Multivariable Aleph-function involving the Generalized Mellin-Barnes Contour Integrals , CUBO, A Mathematical Journal: Vol. 22 No. 3 (2020)
- David Békollè, Khalil Ezzinbi, Samir Fatajou, Duplex Elvis Houpa Danga, Fritz Mbounja Béssémè, Convolutions in \((\mu,\nu)\)-pseudo-almost periodic and \((\mu,\nu)\)-pseudo-almost automorphic function spaces and applications to solve integral equations , CUBO, A Mathematical Journal: Vol. 23 No. 1 (2021)
- Ioannis K. Argyros, Santhosh George, Extended domain for fifth convergence order schemes , CUBO, A Mathematical Journal: Vol. 23 No. 1 (2021)
- Jyotirmoy Mouley, M. M. Panja, B. N. Mandal, Approximate solution of Abel integral equation in Daubechies wavelet basis , CUBO, A Mathematical Journal: Vol. 23 No. 2 (2021)
- N. Seshagiri Rao, K. Kalyani, Fixed point results of \((\phi,\psi)\)-weak contractions in ordered \(b\)-metric spaces , CUBO, A Mathematical Journal: Vol. 24 No. 2 (2022)
- Filippo Cammaroto, Infinitely many solutions for a nonlinear Navier problem involving the \(p\)-biharmonic operator , CUBO, A Mathematical Journal: Vol. 24 No. 3 (2022)
- Ajay Kumar, Ekta Tamrakar, Inertial algorithm for solving split inclusion problem in Banach spaces , CUBO, A Mathematical Journal: Vol. 25 No. 1 (2023)
<< < 10 11 12 13 14 15 16 17 18 > >>
You may also start an advanced similarity search for this article.














