Algorithmic complexity and statistical mechanics
-
Vladimir V'yugin
 vyugin@iitp.ru
vyugin@iitp.ru
-
Victor Maslov
 v.p.maslov@mail.ru
v.p.maslov@mail.ru
Downloads
Abstract
We apply the algorithmic complexity theory to statistical mechanics; in particular, we consider the maximum entropy principle and the entropy concentration theorem for non-ordered data in a non-probabilistic setting. The main goal of this paper is to deduce asymptotic relations for the frequencies of energy levels in a non-ordered collection ωN = [ω1, ..., ωN] from the assumption of maximality of the Kolmogorov complexity K(ωN) given a constraint 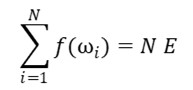 , where E is a number and f is a numerical function; f(ωi) is an energy level. We also consider a combinatorial model of the securities market and give some applications of the entropy concentration theorem to finance.
, where E is a number and f is a numerical function; f(ωi) is an energy level. We also consider a combinatorial model of the securities market and give some applications of the entropy concentration theorem to finance.
Keywords
Similar Articles
- Mohammad Farhan, Edy Tri Baskoro, Further results on the metric dimension and spectrum of graphs , CUBO, A Mathematical Journal: Vol. 28 No. 1 (2026)
- Qilin Xie, Lin Xu, Normalized solutions for coupled Kirchhoff equations with critical and subcritical nonlinearities , CUBO, A Mathematical Journal: Vol. 28 No. 1 (2026)
- Abdelkader Abouricha, Lamya Bouali, Allal Ghanmi, Characterization of bc and strongly bc-polyharmonic functions , CUBO, A Mathematical Journal: Vol. 28 No. 1 (2026)
You may also start an advanced similarity search for this article.













